Yiqing Liang's Blog

Home  /  Blog

The Evolution of Activation Functions: From ReLU to SwiGLU

November 7, 2025 Technical

By Yiqing Liang

Introduction

Activation functions are the unsung heroes of deep learning. While much attention goes to architecture design and training techniques, the choice of activation function profoundly impacts model performance, training stability, and computational efficiency. Over the past decade, we've witnessed a fascinating evolution from simple ReLU to sophisticated gated variants like SwiGLU that power today's largest language models.

In this post, we'll explore the most important activation functions in modern deep learning, understand why certain choices dominate in specific architectures, and examine empirical data on their performance, sparsity patterns, and computational costs.

The Basics: What Makes a Good Activation Function?

Before diving into specific functions, let's establish what we want from an activation function:

  • Non-linearity: Essential for learning complex patterns (otherwise, deep networks collapse to linear models)
  • Gradient flow: Gradients should propagate effectively through deep networks
  • Computational efficiency: Fast to compute in both forward and backward passes
  • No upper saturation: Output can grow without hitting a ceiling, avoiding vanishing gradients (functions like ReLU grow linearly for positive inputs, unlike sigmoid which saturates at 1)
  • Smooth or continuous: Aids optimization (though not strictly necessary, as ReLU shows)
  • Sparsity (optional): Can improve efficiency and interpretability

ReLU: The Foundation

Definition

ReLU(x) = max(0, x)

Why It Won

Introduced by Nair & Hinton (2010) and popularized by AlexNet (2012), ReLU revolutionized deep learning by solving the vanishing gradient problem that plagued sigmoid and tanh activations:

  • No saturation for positive values: Gradient is 1 for x > 0, enabling deep networks
  • Computational simplicity: Just a comparison and zeroing operation
  • Sparsity: Zero neurons can enable sparse computation optimizations (though standard dense implementations still compute zeros)
  • Scale invariance: ReLU(αx) = αReLU(x) for α > 0

Limitations

Despite its success, ReLU has known issues:

  • Dying ReLU problem: Neurons can get stuck at zero with negative inputs, never activating again
  • Not zero-centered: Outputs are always non-negative, which can slow learning
  • Non-smooth at zero: The kink at x = 0 can cause optimization challenges

Widespread Adoption

ReLU became and remains the default choice for many architectures:

  • CNNs: Standard activation in ResNets, VGG, and most convolutional architectures for computer vision
  • Simplicity: Easy to implement and debug, contributing to its widespread adoption
  • Hardware optimization: Modern accelerators (GPUs, TPUs) have highly optimized implementations

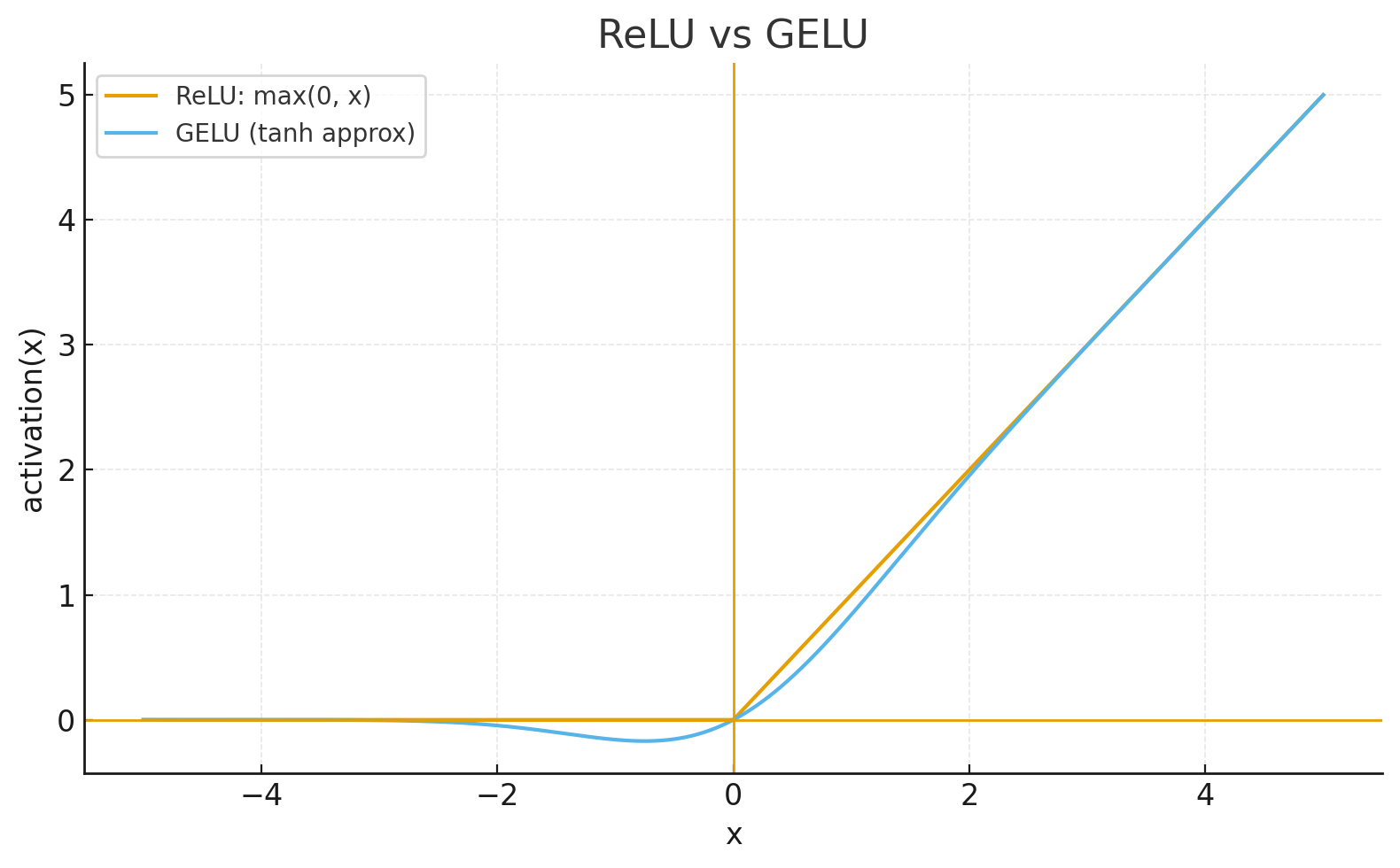
GELU: Smooth Approximation

Definition

Gaussian Error Linear Unit (GELU), introduced by Hendrycks & Gimpel (2016), provides a smooth approximation to ReLU: 

GELU(x) = x · Φ(x)
where Φ(x) is the cumulative distribution function of the standard normal distribution

# Approximation often used in practice:
GELU(x) ≈ 0.5 * x * (1 + tanh(√(2/π) * (x + 0.044715 * x³)))

ReLU vs GELU comparison

Key Properties

  • Smooth everywhere: No kink at zero, better for optimization
  • Better gradient flow: Enabling non-zero gradients for negative inputs (unlike ReLU which has zero gradients)

Transformers Loved GELU

GELU once became the standard activation in transformer models:

Empirical Performance

Practical considerations from the original GELU paper:

  • Compute overhead: More expensive than ReLU due to computing the Gaussian CDF (though approximations help)
  • Sparsity: Lower activation sparsity compared to ReLU since GELU doesn't zero out negative values completely

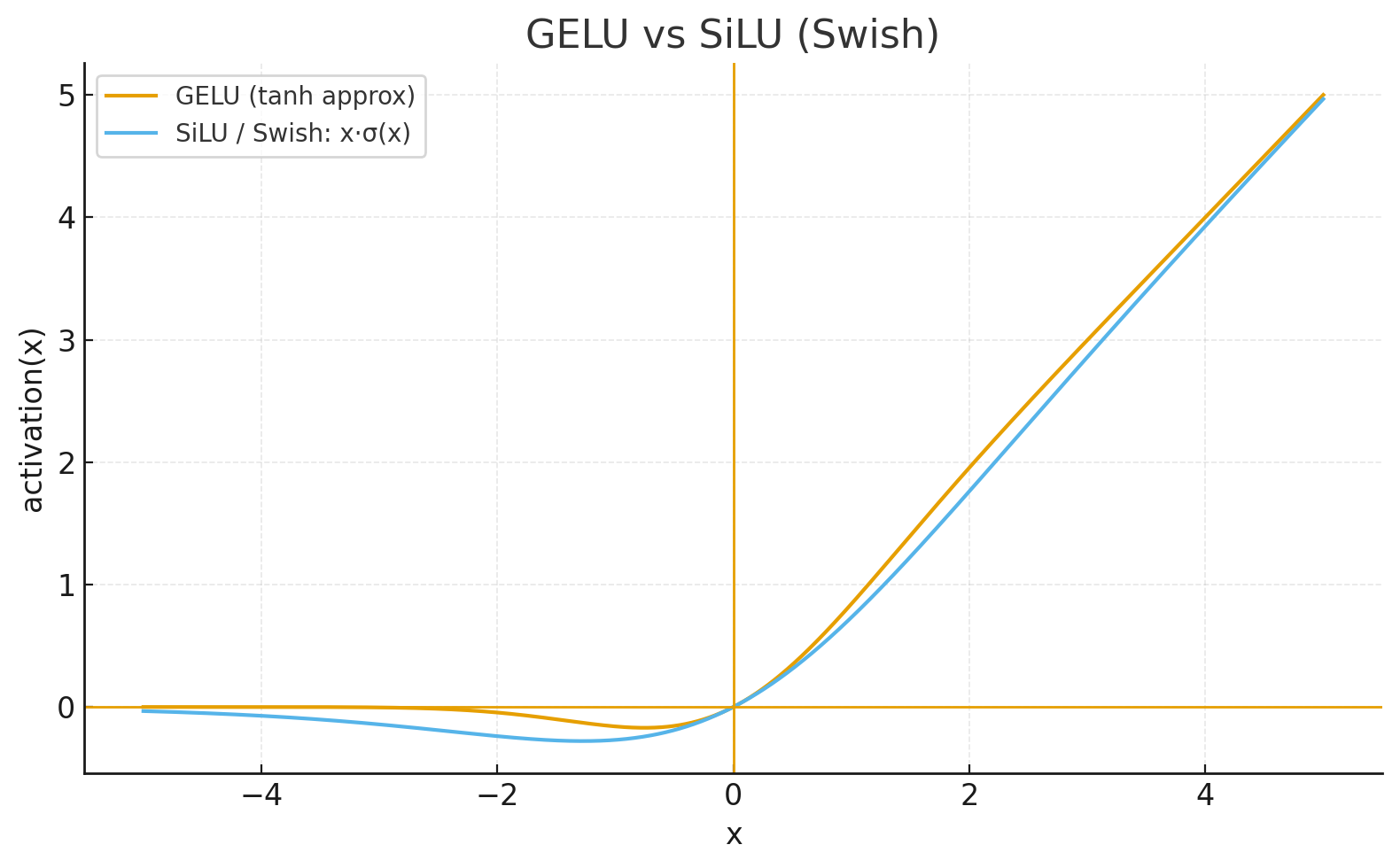
SiLU/Swish: Self-Gated Activation

Definition

Swish (Ramachandran et al., 2017), also known as SiLU (Sigmoid Linear Unit), is a simple self-gated activation: 

Swish(x) = x · σ(x) = x / (1 + exp(-x))

# Parameterized version (β typically learned or set to 1):
Swish_β(x) = x · σ(βx)

Key Properties

  • Smooth and non-monotonic: Similar benefits to GELU
  • Self-gating (bounded below, unbounded above): The input x controls how much of itself passes through via the sigmoid σ(x). When x is large and positive, σ(x) ≈ 1 so the output ≈ x (linear growth, unbounded). When x is large and negative, σ(x) ≈ 0 so the output ≈ 0 (bounded below). This creates adaptive behavior where the activation "decides" based on the input value itself.
  • Nearly identical to GELU: Very similar shapes and empirical performance

GELU vs SiLU/Swish comparison

Empirical Performance

From the Swish paper and EfficientNet:

  • EfficientNet: Uses Swish throughout, achieving SOTA efficiency
  • Compute overhead and Sparsity: SiLU is costlier than ReLU due to sigmoid; exact overhead is kernel-dependent; produces dense activations (no hard zeros).

GLU: The Gating Revolution

Definition

Gated Linear Units (GLU), introduced by Dauphin et al. (2017), brought explicit gating to activations: 

GLU(x, W, V, b, c) = (xW + b) ⊗ σ(xV + c)

where ⊗ means element-wise multiplication (multiply corresponding elements)

# In practice, for input x ∈ ℝ^d, GLU works as follows:
# 1. Linear projection: split input into two parts using different weight matrices
#    - Value path: xW + b (what information to pass)
#    - Gate path: xV + c (how much to pass)
# 2. Apply sigmoid to gate: σ(xV + c) gives values between 0 and 1
# 3. Element-wise multiply: (xW + b) ⊗ σ(xV + c)
#    - Each element in the value is multiplied by corresponding gate value
#    - Gate ≈ 0 blocks information, gate ≈ 1 allows it through

# Simplified notation when input is pre-split into [x₁, x₂]:
GLU([x₁, x₂]) = x₁ ⊗ σ(x₂)
# x₁ is the value (what), σ(x₂) is the gate (how much)

Why Gating Matters

GLU introduced a key insight: learned gating mechanisms can control information flow:

  • Selective activation: Gates determine which information passes through
  • Non-linear interactions: Multiplicative gating creates richer representations
  • Better gradient flow: Linear path through one branch aids backpropagation
  • Adaptive behavior: Gates learn context-dependent activation patterns

Empirical Performance

From the original GLU paper:

  • Parameter efficiency: Better performance with same or fewer parameters
  • Compute overhead: notably more parameters and higher FLOPs vs standard FFN (due to a doubled expand projection)

GLU Variants: ReGLU, SwiGLU, and GeGLU

The Variant Zoo

The success of GLU inspired a natural question: what if we replace the sigmoid function in GLU with other activations? Shazeer (2020) systematically explored this idea: 

# General form of GLU variants:
GLU_variant([x₁, x₂]) = x₁ ⊗ activation(x₂)

# Specific variants:
GLU([x₁, x₂])     = x₁ ⊗ σ(x₂)         # Original (sigmoid)
ReGLU([x₁, x₂])   = x₁ ⊗ ReLU(x₂)      # ReLU gating
GeGLU([x₁, x₂])   = x₁ ⊗ GELU(x₂)      # GELU gating
SwiGLU([x₁, x₂])  = x₁ ⊗ Swish(x₂)     # Swish gating

Empirical Findings

Shazeer's experiments tested these variants in the feedforward layers of Transformer models and found that some variants (particularly GeGLU and SwiGLU) yield quality improvements over the typically-used ReLU or GELU activations.

Adoption in Modern LLMs

Both GeGLU and SwiGLU have been adopted in state-of-the-art language models:

The Shazeer (2020) paper notes that both GeGLU and SwiGLU produce the best perplexities among tested variants, and attributes their success somewhat humorously "to divine benevolence," acknowledging that the precise reasons for their effectiveness remain somewhat unclear.

Why Gated Activations Work

The success of GLU variants (both SwiGLU and GeGLU) can be understood through several mechanisms:

  • Gating mechanism: Allows the network to dynamically control information flow, selectively amplifying important features
  • Smooth gradients: Both Swish and GELU provide smooth, differentiable functions that help gradient flow in deep networks
  • Increased capacity: The gating structure effectively doubles the parameters in the FFN, improving expressiveness
  • Non-monotonicity: Both activation functions are non-monotonic, allowing richer feature representations

Note: The choice between SwiGLU and GeGLU appears largely empirical, with both delivering strong performance. Different research groups and model families have converged on different choices, suggesting the differences may be marginal in practice.

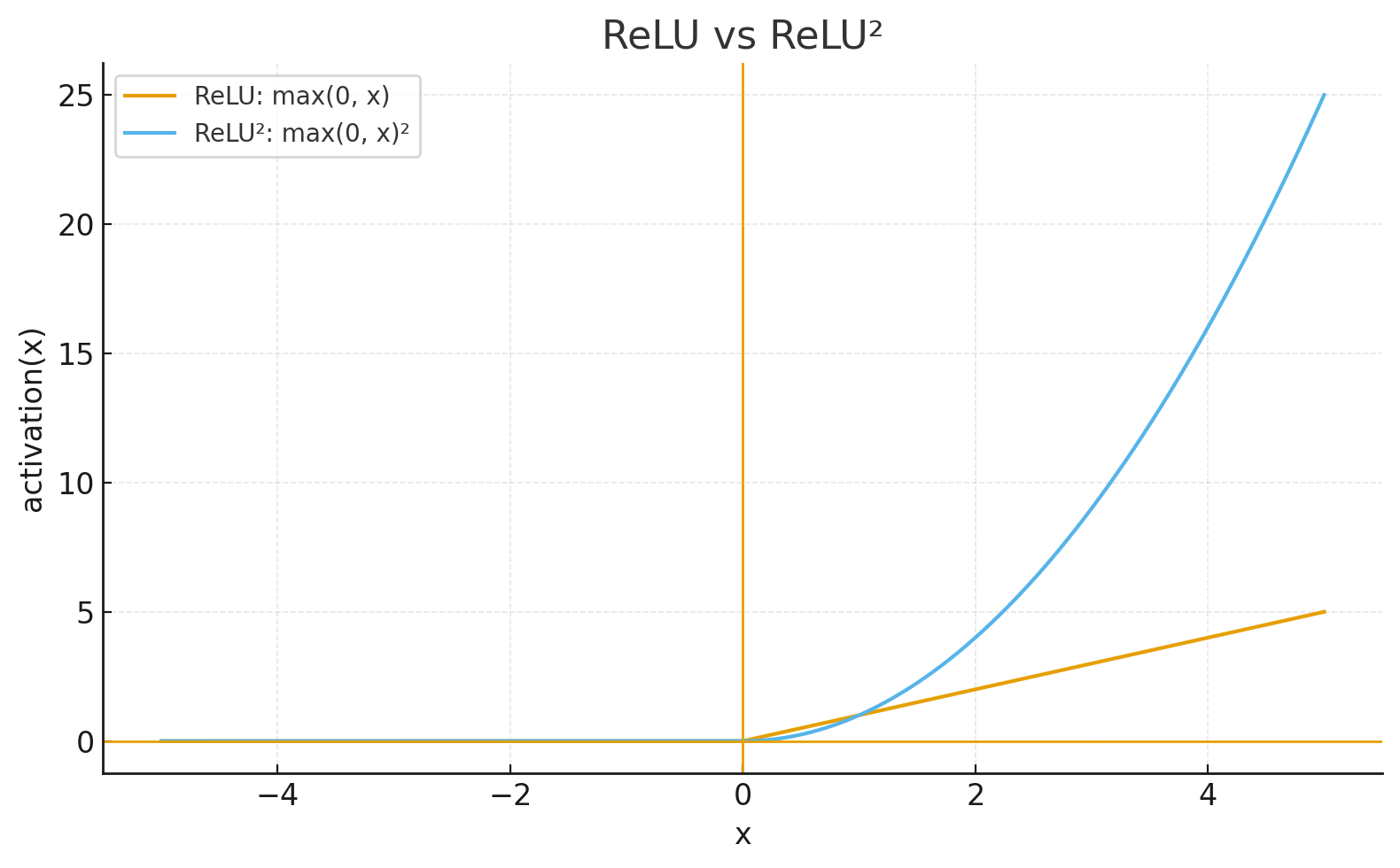
ReLU²: An Alternative to Gated Activations

While GLU variants have gained popularity, they come with 2x parameter overhead. For scenarios where this cost is prohibitive, ReLU² (Squared ReLU) offers an alternative that improves upon standard ReLU without the parameter increase.

Definition

Squared ReLU, introduced in the Primer paper (So et al., 2021): 

ReLU²(x) = (max(0, x))²

ReLU vs ReLU² comparison

Key Properties

  • Increased non-linearity: Squaring amplifies large activations, providing richer representations
  • Maintains sparsity: Still zero for negative inputs, enabling sparse computation
  • No parameter overhead: Unlike GLU variants, doesn't double parameters
  • Simple implementation: Just ReLU followed by squaring, minimal compute cost

Use Cases and Recent Adoption

  • Primer (So et al., 2021): Uses ReLU² in feedforward blocks for efficient transformers
  • ReLU² Wins (Zhang et al., 2024): Systematic study showing ReLU² excels in sparse LLMs across sparsity-performance trade-offs, sparsity predictivity, and hardware affinity
  • PLM-1.8B (2025): 1.8B parameter model using squared ReLU with multi-head latent attention, optimized for edge deployment (mobile phones, Raspberry Pi)
  • Accelerating Transformer Inference and Training with 2:4 Activation Sparsity (Haziza et al., 2025): Leverages squared ReLU's inherent sparsity for GPU-accelerated 2:4 sparsity patterns, achieving 1.3x faster FFN in both forward and backward passes
  • Sparse computation research: ReLU² enables efficient inference through activation sparsity without parameter overhead of GLU variants

Trade-off: ReLU² offers improvements over ReLU with minimal cost, but GLU variants generally provide better performance when parameters and compute are available.

Comparative Analysis: Architecture-Specific Choices

Convolutional Neural Networks (CNNs)

Standard choice: ReLU or Swish

  • ResNets: ReLU remains dominant for its simplicity and speed
  • EfficientNets: Swish provides marginal improvements worth the cost
  • Compute-constrained: ReLU is preferred for its efficiency
  • High-capacity models: Swish or GELU can help squeeze out extra performance

Transformer Language Models

Evolution: GELU → GLU Variants

Early models (2018-2020):

Modern LLMs (2022+):

  • PaLM (540B, 2022) - SwiGLU
  • LLaMA 2 (7B-70B, 2023) - SwiGLU
  • Gemma (2B-7B, 2024) - GeGLU
  • Qwen2 (0.5B-72B, 2024) - SwiGLU

Why the shift to GLU variants:

  • Better performance: Consistent improvements over GELU/ReLU justify the 2x parameter cost at scale
  • Gating mechanism: Dynamic information flow control becomes more valuable in larger models
  • Scaling benefits: Performance gains compound with model size

Vision Transformers

Evolution: GELU → SwiGLU (following language models)

Classic Vision Transformers (GELU):

  • ViT (2020) - GELU
  • CLIP (2021) - GELU
  • DINOv2 (2023) - GELU
  • SAM (Segment Anything, 2023) - GELU

Diffusion Transformers:

  • DiT (Diffusion Transformer, 2023) - GELU/SiLU
  • Hunyuan-DiT (2024) - GELU-approximate

Recent Vision Models with SwiGLU (2024-2025):

  • BAGEL (ByteDance, 2025) - SwiGLU in vision encoders and LLM backbone
  • Llama 3.2-Vision (Meta, 2024) - SwiGLU (32-layer vision encoder + adapter)
  • LoLA-SpecViT (2025) - SwiGLU for hyperspectral imaging
  • Enhanced Swin Transformer (Pacal et al., 2024) - SwiGLU-based MLP for skin cancer diagnosis

The shift to SwiGLU in vision:

  • Following LLM success: Modern multimodal models inherit SwiGLU from their language model backbones
  • Unified architectures: Vision-language models benefit from consistent activation functions across modalities
  • Empirical improvements: Studies show SwiGLU improves accuracy, training speed, and parameter efficiency
  • Recent trend (2024+): New vision transformers increasingly adopt SwiGLU, especially in multimodal contexts

Note: While GELU dominated early vision transformers (2020-2023), the field is shifting toward SwiGLU in modern architectures (2024+), particularly in multimodal and specialized vision models.

Practical Considerations

Sparsity Patterns

  • Exact activation sparsity: ReLU/ReLU² induce hard zeros
  • Dense activations: GELU/SiLU/SwiGLU generally produce non-zero outputs (no hard zeros).

Implementation Tips

# PyTorch implementations

# GELU (use native implementation)
import torch.nn.functional as F
output = F.gelu(x)

# Swish/SiLU (use native implementation)
output = F.silu(x)

# SwiGLU (typical implementation in transformers)
def swiglu(x):
    x, gate = x.chunk(2, dim=-1)
    return x * F.silu(gate)

# Usage in FFN:
# Project to 2*hidden_dim, then apply SwiGLU to get hidden_dim output
ffn_output = W2(swiglu(W1(x)))  # W1: d -> 2*d_ff, W2: d_ff -> d

# ReLU² (simple but effective)
output = F.relu(x) ** 2

Looking Forward: What's Next?

The evolution of activation functions continues:

  • Learned activations: Meta-learning optimal activation shapes for specific tasks
  • Hardware co-design: Activations optimized for specific accelerators (TPUs, specialized AI chips)
  • Sparse activations: Explicit sparsity mechanisms for efficiency (e.g., top-k activation)
  • Adaptive activations: Context-dependent activation functions that change based on input
  • Normalization-free alternatives: Activations that provide built-in normalization properties

Practical Decision Guide

When to Use ReLU

  • Training CNNs for computer vision
  • Compute or memory constrained environments
  • When simplicity and speed are priorities
  • Inference-optimized deployment (sparsity can be exploited)

When to Use GELU/Swish

  • Training transformers (when not using GLU variants)
  • Vision transformers following standard practices
  • When smooth activation is beneficial for optimization
  • Medium to large scale models where compute cost is acceptable

When to Use SwiGLU

  • Training large language models (10B+ parameters)
  • When performance justifies 2x FFN parameter cost
  • Following modern LLM architecture best practices
  • Research or high-capacity scenarios

When to Use ReLU²

  • Experimenting with alternatives to GELU in transformers
  • Want sparsity benefits of ReLU with slightly better performance
  • Minimal compute overhead is critical

Conclusion

The journey from ReLU to SwiGLU reflects deep learning's evolution: from simple, sparse activations optimized for CNNs to sophisticated gated variants that excel in massive transformer models. Key takeaways:

  • ReLU remains king for CNNs: Simple, fast, and effective for convolutional architectures
  • GELU/Swish for smooth optimization: Better gradient flow in transformers, small but consistent improvements
  • SwiGLU for large-scale LLMs: Best performance when parameters and compute are available
  • Context matters: The "best" activation depends on architecture, scale, and constraints

Understanding these activation functions and their trade-offs empowers you to make informed architecture decisions. As models continue to scale and new architectures emerge, activation functions will continue evolving—but the fundamental principles of smooth gradients, computational efficiency, and expressiveness will remain central to their design.

References

Foundational Papers:

Gated Activations:

Modern Architectures:

Language Models:

Vision Models:

Sparse and Efficient Models (ReLU²):

Classic Activations (for context):

← Back to Blog


Home  /  Blog